4211. Бензоколонки

Вдоль кольцевого шоссе длины l расположено n бензоколонок. Если водитель захочет заправиться в некоторой точке шоссе, то он может подъехать к любой бензоколонке, где его с радостью обслужат. Конечно, если бензин вдруг окажется совсем на исходе, водитель, несомненно, поедет к ближайшей бензоколонке, даже если для этого ему придется развернуться назад.

Тем не менее, периодически находятся незадачливые водители, у которых внезапно прямо на трассе бензин заканчивается. Определите максимально возможное расстояние до ближайшей бензоколонки, которое потребуется преодолеть таким водителям пешком.

Вход. В первой строке заданы два целых числа через пробел: длина шоссе l (1 ≤ l ≤ 10⁵) и количество бензоколонок n (1 ≤ n ≤ 10⁴). Во второй строке следуют n различных целых чисел l_i (0 ≤ l_i < l) – позиции бензоколонок.

Выход. Вывести максимально возможное расстояние по шоссе до ближайшей бензоколонки с точностью до 1 десятичного знака.

Пример входа	Пример выхода
5 4 4 0 3 1	1.0

РЕШЕНИЕ

жадные алгоритмы

Анализ алгоритма

Когда у водителя закончится бензин, он может двигаться либо вперед, либо назад по шоссе. Если расстояние между некоторыми соседними бензоколонками равно d, и водитель станет на шоссе где-то между ними, то в худшем случае (если бензин закончится как раз посередине) ему придется пройти расстояние d / 2. Остается найти наибольшее расстояние между всеми соседними бензоколонками и разделить его на 2.

Пусть l₁ и l_n – соответственно позиции первой и последней бензоколонок. Поскольку шоссе кольцевое и его длина равна l, то расстояние между первой и последней бензоколонками равно l – l_n + l₁.

Пример

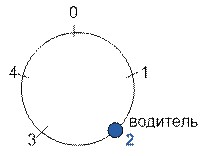
Рассмотрим пример, приведенный в условии. Наибольшее растояние достигается между бензоколонками в позициях 1 и 3. Оно равно d = 2. В худшем случае водителю придется пройти до ближайшей бензоколонки расстояние d / 2 = 1.

Реализация алгоритма

Позиции бензоколонок будем хранить в массиве dist.

#define MAX 10001

int dist[MAX];

Читаем входные данные.

scanf("%d %d",&l,&n);

for(i = 1; i <= n; i++)

scanf("%d",&dist[i]);

Отсортируем входные позиции бензоколонок dist[1], …, dist[n].

sort(dist+1,dist+n+1);

Ищем наименьшее расстояние между соседними бензоколонками с учетом того, что они расположены по кругу. Расстояние между первой и последней бензоколонкой, являющимися соседними, равно l – dist[n] + dist[1]. Далее при вычислении минимума учитываются разности dist[2] – dist[1], …, dist[n] – dist[n – 1].

res = l - dist[n] + dist[1];

for(i = 1; i < n; i++)

res = max(res,dist[i+1] - dist[i]);

Выводим найденный ответ – половину наименьшего расстояния между соседними бензоколонками.

printf("%.1lf\n",res/2.0);